続*4：2次元イジングモデル - おいも貴婦人ブログ

2次元イジングモデルでの各ステップでのアップデート方法に致命的な部分がありました...。

今までの2次元イジングモデルのアップデート方法（１）

2次元上のスピンをランダムに一つ選び、スピンを反転させる。
前状態とのエネルギー差を計算する。
メトロポリス法に従い、状態をアップデートするか決める。

詳細釣り合いの条件さえ満たせばいいので、1.のランダムに１つスピンを選ぶ必要はありません(詳細釣り合いの条件は2.,3.にしか関係がない)。そのため、スピンの通し番号を付けたとすると、1,2,3,...,nのスピンを順番に反転させ、エネルギー差を計算し、メトロポリス法に従い、状態の遷移を決定しても良いのです。まとめると

修正版の2次元イジングモデルのアップデート方法（２）

i=1からスピンの総数
1. iのスピンを反転させる。
2. 前状態とのエネルギー差を計算する。
3. メトロポリス法に従い、状態をアップデートするか決める。

となります。この方法の方がメジャーだと思います。

どうして修正版の方が良いのか。

一見、（１）と（２）の計算量は変わらないように見えます。実際にその通りです。計算量は変わらないのですが、（２）は容易に並列化をすることができます。

Checkerboard decomposition

f:id:oimokihujin:20151112231614p:plain
(from wikipedia(この画像の引用))
今、80x80の要素を持つ２次元イジングモデルを上手のように分割します。つまり、a8の要素には10x10のスピンが存在します。a8のスピンをアップデートするときに隣り合うスピンは、周期境界条件を用いたとすると、a1,a7,b8,h8に存在します。こう考えると、薄いタイルはそれぞれ独立にアップデート可能です。つまり薄いタイルを計算するときは並列化可能です。次に、濃いタイルをアップデートします。

薄いタイルを計算する。(並列化可能)
濃いタイルを計算する。(並列化可能)

（１）の方法で並列化しない理由

特に理由はありません。そもそもランダムに一つ選ぶ必要がない（詳細釣り合いの条件に影響を与えない）ので、そのステップを省略する形になっています。

pythonでのプログラム（並列化はしていません）

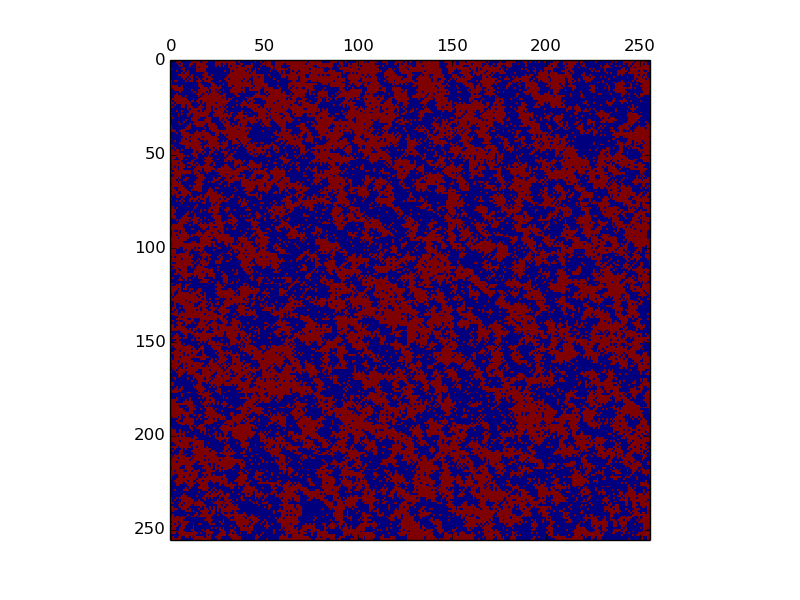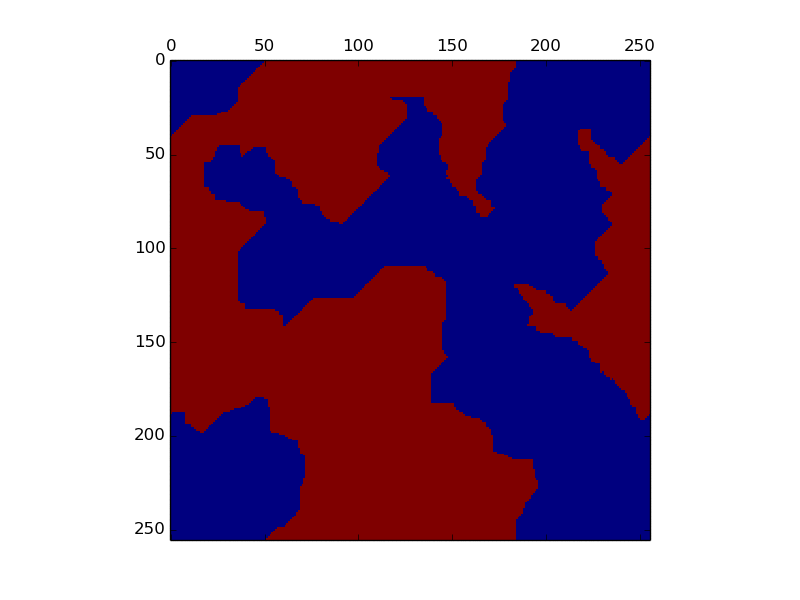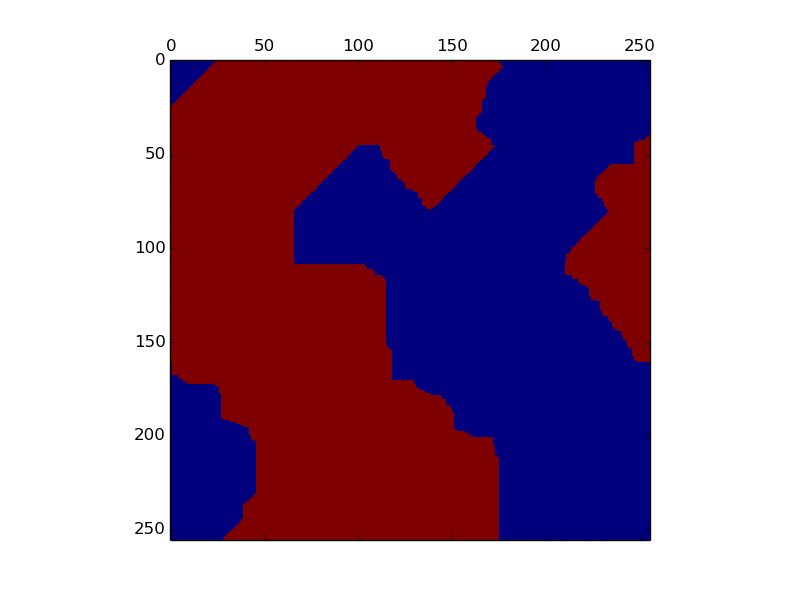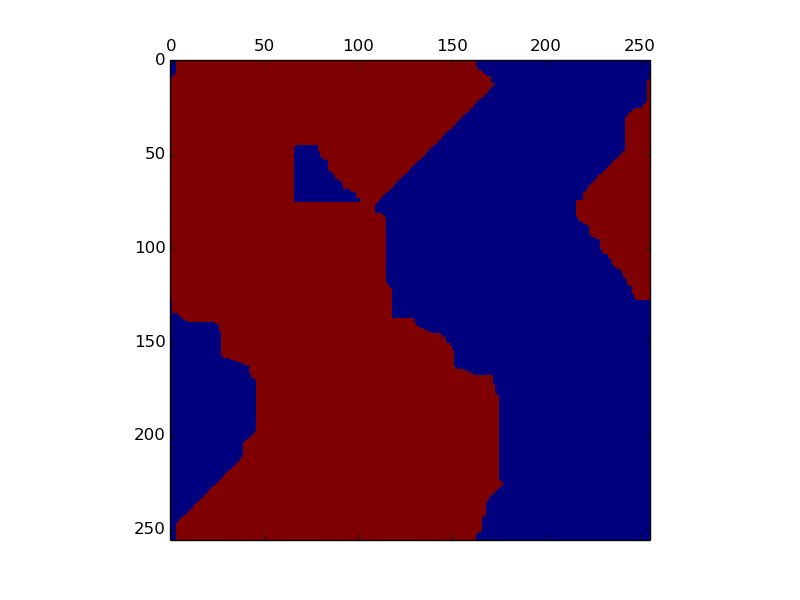
256x256のイジングモデルを100ステップ計算してみました。総ステップ数は256x256x100(6,553,600ステップ)になります。前回のプログラムのMCの部分を以下に書き換えます。

    def simulate(self,loop):
        E = self.calcE(self.xy)
        for i in xrange(loop):
            for x in xrange(self.dimx):
                for y in xrange(self.dimx):
                    dE = self.calcDeltaE([x,y])
                    if dE<=0:
                        self.xy[x][y] = -self.xy[x][y]
                        E+=dE
                    else:
                        pro = np.random.random()
                        if pro < np.exp(-(dE)/self.T):
                            self.xy[x][y] = -self.xy[x][y]
                            E+=dE
                    print E
            self.show(i)

f:id:oimokihujin:20151113003652g:plain

結果

環境(256*256サイズ)	python
Time	1m20.770s